Algorithm example 3 - Ray sphere intersection
Intersection test between a ray and a sphere will be an example of algebraic geometry. Inserting a general line equation:
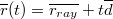
Into sphere surface equation:
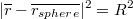
Gives a quadratic equation for t in terms of the known input vectors and R. In code the solution for t can be implemented as follows:
inline bool intersect(const vec3& raydir, const vec3& rayorig,const vec3& pos,
const float& rad, vec3& hitpoint,float& distance, vec3& normal)
{
float a = sum(raydir*raydir);
float b = sum(raydir * (2.0f * ( rayorig - pos)));
float c = sum(pos*pos) + sum(rayorig*rayorig) -2.0f*sum(rayorig*pos) - rad*rad;
float D = b*b + (-4.0f)*a*c;
// If ray can not intersect then stop
if (D < 0)
return false;
D=sqrtf(D);
// Ray can intersect the sphere, solve the closer hitpoint
float t = (-0.5f)*(b+D)/a;
if (t > 0.0f)
{
distance=sqrtf(a)*t;
hitpoint=rayorig + t*raydir;
normal=(hitpoint - pos) / rad;
}
else
return false;
return true;
This can be vectorized for example by intersecting a packet of four rays against a single sphere. The other possibility is to intersect a single ray against four spheres. There is control logic in the code, which has to be replaced by mask operations. Additionally the vectorized intersection function will be taking a mask, which determines which rays should be touched by the function in the first place. An implementation follows:
inline vec4b intersect(const mat4x3& raydir, const mat4x3& rayorig, const vec3& pos,
const float& rad, mat4x3& hitpoint, vec4& distance, mat4x3& normal, vec4b& mask)
{
vec4 raydirx = raydir[0];
vec4 raydiry = raydir[1];
vec4 raydirz = raydir[2];
vec4 a = raydirx*raydirx + raydiry*raydiry + raydirz*raydirz;
vec4 rayorigx = rayorig[0];
vec4 rayorigy = rayorig[1];
vec4 rayorigz = rayorig[2];
vec4 b = raydirx * 2.0f * (rayorigx - pos[0]) +
raydiry * 2.0f * (rayorigy - pos[1]) + raydirz * 2.0f * (rayorigz - pos[2]);
vec4 c = sum(pos*pos) + rayorigx*rayorigx + rayorigy*rayorigy + rayorigz*rayorigz -
2.0f*(rayorigx*pos[0] + rayorigy*pos[1] + rayorigz*pos[2]) - rad*rad;
vec4 D = b*b + (-4.0f)*a*c;
mask = mask && D > 0.0f;
if (ForWhich(mask) == 0)
return mask;
D = Sqrt(D);
vec4 t = (-0.5f)*(b+D)/a;
mask = mask && t > 0.0f;
int bitmask = ForWhich(mask);
// All rays hit
if (bitmask == 15)
{
distance = Sqrt(a) * t;
vec4 hitpointx = rayorigx + t*raydirx;
vec4 hitpointy = rayorigy + t*raydiry;
vec4 hitpointz = rayorigz + t*raydirz;
normal[0]=(hitpointx - pos[0]) / rad;
normal[1]=(hitpointy - pos[1]) / rad;
normal[2]=(hitpointz - pos[2]) / rad;
hitpoint[0]=hitpointx;
hitpoint[1]=hitpointy;
hitpoint[2]=hitpointz;
}
else if (bitmask == 0)
return mask;
else // some rays hit
{
distance = Condition(mask, Sqrt(a) * t, distance);
vec4 hitpointx = rayorigx + t*raydirx;
vec4 hitpointy = rayorigy + t*raydiry;
vec4 hitpointz = rayorigz + t*raydirz;
normal[0]=Condition(mask, hitpointx - pos[0], normal[0]);
normal[1]=Condition(mask, hitpointy - pos[1], normal[1]);
normal[2]=Condition(mask, hitpointz - pos[2], normal[2]);
hitpoint[0]=Condition(mask, hitpointx, hitpoint[0]);
hitpoint[1]=Condition(mask, hitpointy, hitpoint[1]);
hitpoint[2]=Condition(mask, hitpointz, hitpoint[2]);
}
return mask;
}
Note how the last part of the code had to be divided into three sections, one for when all rays hit, one where part of them hit and one where none of them hit. The Condition and ForWhich functions are part of Veclib and documented by it.
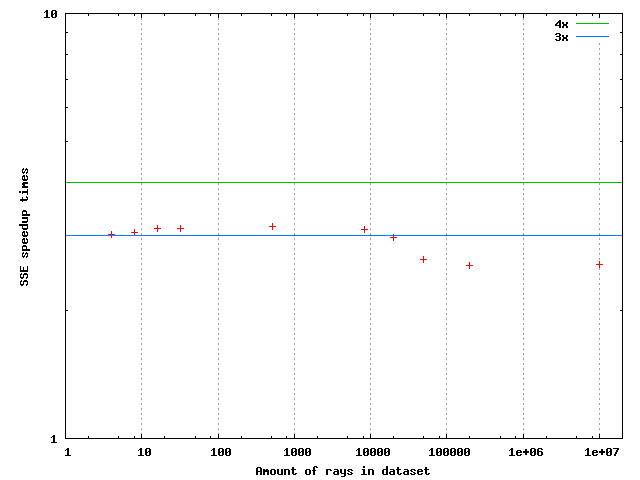
For this algorithm I was unable to get a speedup approaching 4x when all rays were coherent and hit. The vectorized algorithm looks fine as does the machine code output. A figure of the speedup behavior follows: