Algorithm example 2 - N-particle dynamics
N particles where each particle interacts with all the other particles through a force and the motion is solved by numerical integration. In scalar code this can be effectively solved by defining a Particle class as follows and then executing the force member function once to each pair of particles:
class Particle {
public:
vec3 pos;
vec3 vel;
vec3 acc;
float mass;
Particle(vec3 pos, vec3 vel, float mass)
{
Particle::pos=pos;
Particle::vel=vel;
Particle::acc=0.0f;
Particle::mass=mass;
}
/** Newton's gravitation law */
void force(Particle& p)
{
vec3 diff = pos - p.pos;
float r2=sum(diff*diff);
diff /= sqrt(r2)*(r2+1.0f);
acc -= diff*p.mass;
p.acc += diff*mass;
}
};
Forces between all the particles can then be solved and a very basic numerical integration implemented as follows:
std::vector<Particle> data1;
// Iterate the following code in a loop
for (int i=0;i<data1.size();i++)
data1[i].acc=0.0f;
for (int i=0;i<data1.size();i++)
for (int j=i+1;j<data1.size();j++)
data1[i].force(data1[j]);
for (int i=0;i<data1.size();i++)
{
data1[i].vel += data1[i].acc*dt;
data1[i].pos += data1[i].vel*dt;
}
To transform this into SIMD concept by taking note of SSE alignment requirements we can think as follows: Store four particles in a single structure so that everything that is done for a single particle can be done in parallel to four particles. However, calculating the forces between all the particles isn't anymore as straightforward as force has to be calculated between all particles and not just between particles of different packets. The solution is to calculate the forces to each individual particle from all other packets and additionally from particles in the same packet. The following is an implementation of this concept:
class Particle4 {
public:
mat4x3 pos;
mat4x3 vel;
mat4x3 acc;
vec4 mass;
Particle4(mat4x3 pos, mat4x3 vel, vec4 mass)
{
Particle4::pos=pos;
Particle4::vel=vel;
Particle4::acc=0.0f;
Particle4::mass=mass;
}
/// Calculate forces to each member Particle from another Particle4
void force(Particle4& p)
{
for (int n=0;n<4;n++)
{
vec4 diffx = vec4(pos[0][n]) - p.pos[0];
vec4 diffy = vec4(pos[1][n]) - p.pos[1];
vec4 diffz = vec4(pos[2][n]) - p.pos[2];
vec4 r2 = diffx*diffx + diffy*diffy + diffz*diffz;
vec4 rlen = 1.0f/(Sqrt(r2)*(r2+1.0f));
diffx *= rlen;
diffy *= rlen;
diffz *= rlen;
acc[0][n] -= sum(diffx*p.mass);
acc[1][n] -= sum(diffy*p.mass);
acc[2][n] -= sum(diffz*p.mass);
p.acc[0] += diffx*mass;
p.acc[1] += diffy*mass;
p.acc[2] += diffz*mass;
}
}
/// Calculate forces between particles inside this Particle4
void insideforces(void)
{
for (int n=0;n<4;n++)
for (int k=n+1;k<4;k++)
{
vec3 diff;
diff[0] = pos[0][n] - pos[0][k];
diff[1] = pos[1][n] - pos[1][k];
diff[2] = pos[2][n] - pos[2][k];
float r2=sum(diff*diff);
diff /= sqrt(r2)*(r2+1.0f);
acc[0][n] -= diff[0]*mass[k];
acc[1][n] -= diff[1]*mass[k];
acc[2][n] -= diff[2]*mass[k];
acc[0][k] += diff[0]*mass[n];
acc[1][k] += diff[1]*mass[n];
acc[2][k] += diff[2]*mass[n];
}
}
};
And solving the motions is implemented then by:
std::vector<Particle4> data2;
// Repeat for number of iterations
for (int i=0;i<data2.size();i++)
data2[i].acc=0.0f;
for (int i=0;i<data2.size();i++)
{
data2[i].insideforces();
for (int j=i+1;j<data2.size();j++)
data2[i].force(data2[j]);
}
for (int i=0;i<data2.size();i++)
{
data2[i].vel += data2[i].acc*dt4;
data2[i].pos += data2[i].vel*dt4;
}
Note that everything except calculation of the forces inside a Particle packet could be vectorized. The speedup from this implementation was at best close to exactly 2x. Not quite satisfactory. In this implementation the forces are calculated from each N packets to the first, second, third and fourth particle inside Particle4 in turn. However, calculating forces to the first particle from all the other packets and then repeating for the three more particles, it is possible to get rid the horizontal sums "sum(diffx*p.mass)" and scalar extracts "vec4(pos[0][n])" from the Particle4 force function. The implementation is modified then as follows:
// Replacement force function for NParticle
void force(NParticle& p, const vec4& posx, const vec4& posy, const vec4& posz, vec4& accx, vec4& accy, vec4& accz)
{
vec4 diffx = posx - p.pos[0];
vec4 diffy = posy - p.pos[1];
vec4 diffz = posz - p.pos[2];
vec4 r2 = diffx*diffx + diffy*diffy + diffz*diffz;
vec4 rlen = 1.0f/(Sqrt(r2)*(r2+1.0f));
diffx *= rlen;
diffy *= rlen;
diffz *= rlen;
accx -= diffx*p.mass;
accy -= diffy*p.mass;
accz -= diffz*p.mass;
p.acc[0] += diffx*mass;
p.acc[1] += diffy*mass;
p.acc[2] += diffz*mass;
}
and force calculation:
// Replacement for force calculations
for (int i=0;i<data2.size();i++)
{
data2[i].insideforces();
for (int n=0;n<4;n++)
{
vec4 posx = data2[i].pos[0][n];
vec4 posy = data2[i].pos[1][n];
vec4 posz = data2[i].pos[2][n];
vec4 accx=0.0f;
vec4 accy=0.0f;
vec4 accz=0.0f;
for (int j=i+1;j<data2.size();j++)
data2[i].force(data2[j],posx,posy,posz,accx,accy,accz);
data2[i].acc[0][n] += sum(accx);
data2[i].acc[1][n] += sum(accy);
data2[i].acc[2][n] += sum(accz);
}
}
This implementation is much faster. The speed gain is represented in the following figure:
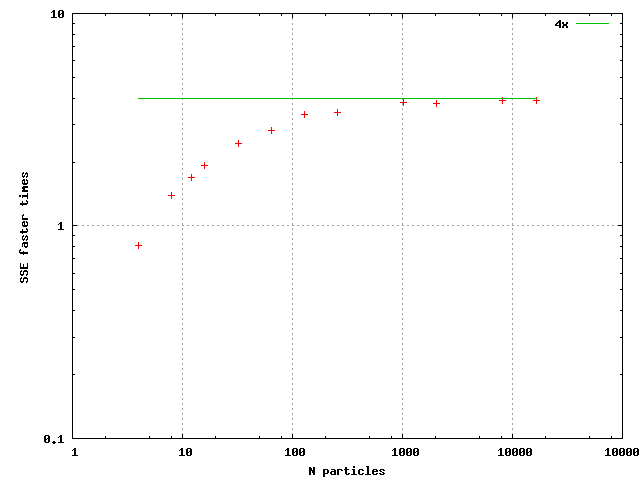
The output was not generally bit wise identical because floating point operations are carried out in different order between the paths. However, calculation precision in both paths is the same. One more additional note is that using the SSE3 haddps inctruction for the horizontal sum made barely any difference to using SSE2 style horizontal sum.