Algorithm example 1 - Vector normalization
As noted in the chapter about data structures, vector normalization can be implemented with SSE in a very straightforward manner:
// Example one. Normalizing AOS vectors
// Scalar
inline void normalize(std::vector<vec3>& data)
{
for (int i=0;i<data.size();i++)
{
vec3& m = data[i];
m /= sqrtf( m[0]*m[0] + m[1]*m[1] + m[2]*m[2] );
}
}
// SSE
inline void normalize(std::vector<mat4x3>& data)
{
for (int i=0;i<data.size();i++)
{
vec4 mx = data[i][0];
vec4 my = data[i][1];
vec4 mz = data[i][2];
vec4 multiplier = 1.0f/Sqrt(mx*mx + my*my + mz*mz);
mx*=multiplier;
my*=multiplier;
mz*=multiplier;
data[i][0]=mx;
data[i][1]=my;
data[i][2]=mz;
}
}
In the scalar version the explicit loading and unloading of data to and from memory to temporary variables could be avoided notationally by using a vec3 reference. However, in the SSE version vec4 temporary types must be used in order to make compiler produce optimal code. In practice these temporaries will be XMM registers in the assembly code produced. Note that using the mat4x3 type as a reference this could be written in the SSE version as:
// SSE (wrong, mat4x3 elements referenced multiple times)
inline void normalize(std::vector<mat4x3>& data)
{
for (int i=0;i<data.size();i++)
{
mat4x3& m = data[i];
m /= Sqrt(m[0]*m[0] + m[1]*m[1] + m[2]*m[2]);
}
}
However, compiler doesn't produce optimal instructions this way. It is able to do so with the scalar version I believe because of the C++ expression templates behind cvalarray implementation of vec3.
Taking a look at what kind of instructions GCC 4.4.2 produces for these here is first the scalar version:
movss (%rax), %xmm3
movss 4(%rax), %xmm2
movss 8(%rax), %xmm1
movaps %xmm2, %xmm0
movaps %xmm3, %xmm4
mulss %xmm2, %xmm0
mulss %xmm3, %xmm4
addss %xmm4, %xmm0
movaps %xmm1, %xmm4
mulss %xmm1, %xmm4
addss %xmm4, %xmm0
movaps %xmm5, %xmm4
sqrtss %xmm0, %xmm0
divss %xmm0, %xmm4
movaps %xmm4, %xmm0
mulss %xmm4, %xmm3
mulss %xmm4, %xmm2
movss %xmm3, (%rax)
movss %xmm2, 4(%rax)
mulss %xmm1, %xmm0
movss %xmm0, 8(%rax)
And here the SSE:
movaps (%rax), %xmm3
movaps 16(%rax), %xmm2
movaps 32(%rax), %xmm1
movaps %xmm2, %xmm5
movaps %xmm3, %xmm0
mulps %xmm2, %xmm5
mulps %xmm3, %xmm0
movaps %xmm1, %xmm4
addps %xmm5, %xmm0
mulps %xmm1, %xmm4
addps %xmm4, %xmm0
movaps %xmm6, %xmm4
sqrtps %xmm0, %xmm0
divps %xmm0, %xmm4
movaps %xmm4, %xmm0
mulps %xmm4, %xmm3
mulps %xmm4, %xmm2
mulps %xmm1, %xmm0
movaps %xmm3, (%rax)
movaps %xmm2, 16(%rax)
movaps %xmm0, 32(%rax)
One can notice definitive symmetry between the two even if one understands little to no x86. There are only aligned 128-bit moves in the SSE version and it is almost identical to the scalar version except for packaged instructions instead of scalar, which is a sign of proper code generation by the compiler.
It is worth the effort to go through either version instruction by instruction to be able to understand if the instruction output makes sense or not. This helps with debugging SSE applications tremendously. Definitions of each instruction can be found by a web search.
It is very educational to also look at the "wrong" version:
movaps 32(%rax), %xmm1
movaps 16(%rax), %xmm2
movaps (%rax), %xmm3
movaps %xmm1, %xmm4
movaps %xmm2, %xmm5
mulps %xmm1, %xmm4
mulps %xmm2, %xmm5
movaps %xmm3, %xmm0
mulps %xmm3, %xmm0
addps %xmm5, %xmm0
addps %xmm4, %xmm0
sqrtps %xmm0, %xmm0
divps %xmm0, %xmm3
divps %xmm0, %xmm2
movaps %xmm3, (%rax)
movaps %xmm2, 16(%rax)
divps %xmm0, %xmm1
movaps %xmm1, 32(%rax)
In this case there is actually nothing wrong with it, except it does what was asked: It performs three divisions instead of three multiplications in the end, which slows it down. Replacing /= with *= and adding 1.0f/ results in yet another version:
movaps (%rax), %xmm3
movaps 32(%rax), %xmm1
movaps 16(%rax), %xmm2
mulps %xmm1, %xmm1
movaps %xmm3, %xmm0
mulps %xmm2, %xmm2
mulps %xmm3, %xmm0
addps %xmm2, %xmm0
addps %xmm1, %xmm0
movaps %xmm4, %xmm1
sqrtps %xmm0, %xmm0
divps %xmm0, %xmm1
movaps %xmm1, %xmm0
mulps %xmm1, %xmm3
mulps 32(%rax), %xmm0
mulps 16(%rax), %xmm1
movaps %xmm3, (%rax)
movaps %xmm1, 16(%rax)
movaps %xmm0, 32(%rax)
The problem with this one is that it once again does what was asked: It performs the multiplication "mulps 32(%rax), %xmm0" not with purely XMM registers. These two cases should help to illustrate why it is unfortunately necessary to explicitly tell the compiler what to do when dealing with vec4 types. Problems can be usually avoided by not using the mat4x3 type as a reference or worst as a temporary. It should only be used for loading and extracting data at the start and end of a function or more optimally the longest possible code block.
It is also of interest to look at the speed gains from SSE from this implementation. The test hardware is Intel Core 2 Duo E6400. Operating system is 64-bit Linux and the compiler is GCC 4.4.2.
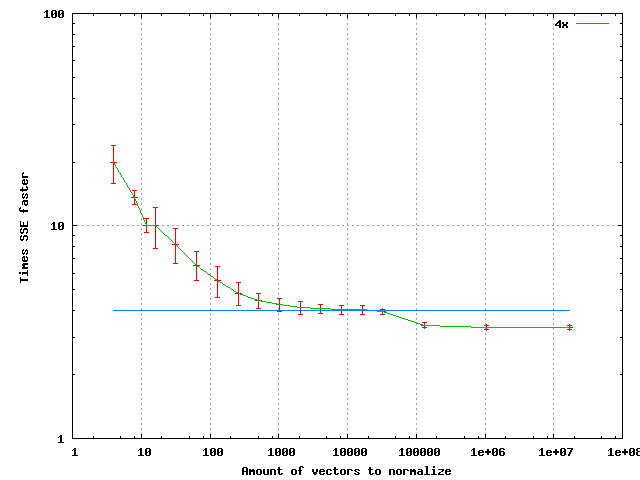
The points are sample means and the standard error tells how the samples were spread. If the functions are forced not to be inlined then the > 4x behavior for N < 10000 disappears. Here we can see a speedup of very close to 4x for normalizing a set of about 20000 vectors. At very large amounts the speedup settles to about 3.4x. As for the reason of the general shape of the curve, anyone is welcome to make a guess. The output between SSE and scalar paths is identical bit to bit.
If normalizing the same data of vectors over and over multiple times the speedup from SSE was about 2.7x-2.2x when number of repetitions is large. The larger speedup applies to data sets smaller than about 20000 and the smaller for larger data sets. This is I believe because the data was moved between memory and registers between each normalization and for some reason this penalizes the SSE implementation more.